索引 - 索引快的原理 ¶
作者:KK
发表日期:2017.6.6
要点速读 ¶
本文主要针对菜鸟程序员编写,让大家了解索引的大概原理、索引为什么要重构、如何考虑使用索引,高手可以略过
MySQL的索引是通过一种叫B+Tree的数据结构实现的,大学的同学们在一年级入门时应该都有接触过它的祖先二叉树
假设有1000行数据,MySQL可以在B+Tree树中跳转几次就能找到需要的数据在哪一行了,所以索引能为查询节省时间
每种表引擎的具体索引实现原理都不尽相同,通常大家都谈论MyISAM引擎与InnoDb引擎的索引实现
二叉树有很多种演变体,大部分数据库都使用B+Tree这种(二叉树的变种)来实现搜索,而MyISAM和InnoDb的B+Tree都有各自的细节定制修改,导致了两种表引擎各有异同,适用不同的场景
简单的二叉树示例 ¶
二叉树有很多种,B+Tree由平衡二叉树演变得来,我这里只是简单介绍这种树,让大家能理解索引的主要原理和问题
首先抛出一个小考题:有23、77、89、22、34、5、91共7个数字牌,如果让你保管好,你怎么保管才能在需要的时候快速找出指定的号码牌呢?
你的答案我就不听了,我是这样存的:
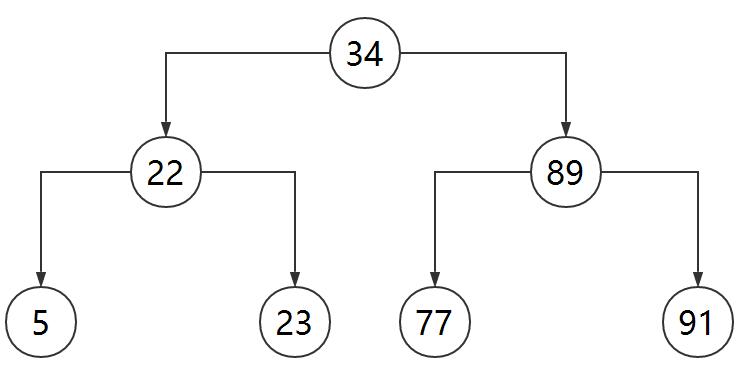
这是一个树状结构的保存形式(所谓二叉树就是节点上有2个叉,你理解为有2个分支就好了),保存的逻辑是:
先找出所有数字里面的中间数放在最顶上作为根节点,于是34号就在最顶上了
把小于34的放在左边,大于34的放在右边
先说34的左边,这里它要建立34左边的下一级节点,这个节点用哪个数字呢?于是又从这堆小于34的数字(5、22、23)里找一个中间数,所以是22
小于22的5又放22的左边,大于22的23又放在它的右边
回到根节点,34的右边也是一样的逻辑,从大于34的数字里找一个中间数得到89
小于89的77放在左边,91放在右边
这样就建立了一个二叉树数据结构,其实二叉树主要用来实现搜索功能,这是它出了名的作用,于是我们开始举一个搜索的例子吧
如果要找77号的话,从根节点开始找,我发现它大于34号,于是忽视掉所有34左边的号码,直接往右边走,这样就过滤掉了一半的数字对不对?
右边下一级遇到了89,目标数77比89小,于是往左走,就找到了77
查找原则就是:从上到下查找,目标数字比节点上的数字小就往左,否则就往右
我用JS代码模拟一下这个情况:
//模拟二叉树,这里为每个节点增加一个唯一的ID值
var tree = {
id : 2,
value : 34,
left : {
id : 6,
value : 22,
left : {
id : 7,
value : 5
},
right : {
id : 3,
value : 23
}
},
right : {
id : 4,
value : 89,
left : {
id : 1,
value : 77
},
right : {
id : 5,
value : 91
}
}
};
//查找函数,返回节点的ID
function searchTree(value, tree){
if(tree.value === value){
return tree.id;
}
if(tree.left && value < tree.value){
//小于该节点就往左查
return searchTree(value, tree.left);
}else if(tree.right && value > tree.value){
//大于该节点就往右查
return searchTree(value, tree.right);
}else{
return null;
}
}
searchTree(77, tree); //ID为1
searchTree(23, tree); //ID为3
searchTree(777, tree); //null 搜索失败
再来一个例子,如果存了1到99999这些数字,要找出13451这个数字
中间数是49999嘛,只要13451比49999小,于是往左
左边又会遇到下一级的中间数24999,再往左
下一级中间数是12499,目标13451比它大,于是往右
下一级中间数是……
跳转没多久就找到它了,不然如果你从1到99999这样for循环遍历的话是不是要遍历13451次才找到了它?这样就没效率了
MySql的索引大概是这样的 ¶
哈,这是我做的菜鸟阅读版,不是真实的版本,免得太复杂了难理解
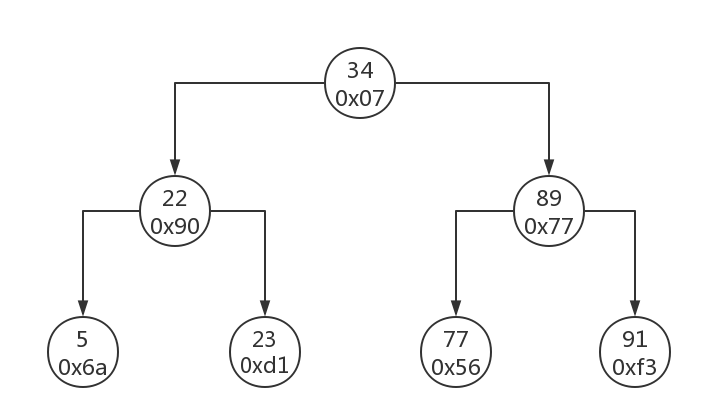
这里每个节点的值下面都多了一个16进制的地址,其实它是一个磁盘地址。
再看下图,假设我们建立一个user表的时候,如果设定了id和age两个字段,其实有一个我们看不到的东西就是磁盘地址,下图是数据表的形态
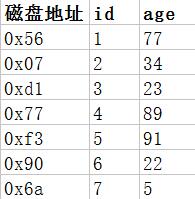
计算机的数据存放在磁盘上(包括MySQL的数据),磁盘上每一个储存单元(叫扇区)都是有一个地址的
比如我们可以抽象地说var 数据 = 磁盘.read(0x18db3a, 1024)这样就是传递一个磁盘地址,要求磁盘从这个地址开始读取1024个字节数据出来,所以MySQL的数据存在磁盘里自然也需要磁盘地址才能读取数据
那么问题来了:MySQL只是个软件而不是硬盘,它管不了磁头读数据的行为,但为了实现高效的数据查询,就要想办法快速地知道要读取的数据在哪个磁盘地址
于是就像上面的例子,用二叉树数据结构建立一个索引,当WHERE子句的条件出现age字段时,就往age的索引(二叉树)里找这些age对应记录行的磁盘地址
假如没有索引,扫全表是痛苦的 ¶
你想想如果没有索引会多么痛苦哦,上面表格中id为7的记录在最后嘛,那如果SELECT * FROM user WHERE age = 5的时候,不用索引的话就只能扫全表了,代码示例:
var 所有记录 = MySql系统.读出所有表数据('user');
var result = [];
for(var i in 所有记录){
var 数据记录 = 所有记录[i];
if(数据记录.age == where.age){
result.push(数据记录);
}
}
return result;
虽然这个代码写得很不真实,而且有点多余的样子,但这里我要强调的是全表扫描,数据那么多,扫到最后一条记录才发现age = 5的数据,耗费是多么巨大呢?所以在优化查询的过程中,首先就要尽量避免全表扫描;而利用二叉树结构的索引来查找,没多久就能找到需要的值
索引重构 ¶
这里我们再重复看一下上面的二叉树:

假如执行INSERT INTO user(id, age) VALUES(8, 77);这样的时候,数据表当然就多了一条记录,可是如果依然用上面这棵树去搜索会发现找不到77这个age值——因为这棵树是旧的,没有记录新的age所在行数据的磁盘地址
所以接下来就要做这么一件事:对索引进行重构工作,也就是二叉树的重构,重构后得到下面这样一棵新树才能从中搜索到age=77

而在新的结构中也可以发现,根节点成了77,因为在插入82后,5、22、23、34、77、82、89、91这些数字的中间数就是77
77下面的节点结构也跟前面的不同了,这种旧树到新树的形态变化过程也叫做二叉树的旋转
每当数据有变化的时候(也就是增、删、改的时候),就需要重构索引,所以对于经常变动的数据不适宜建索引,比如用户积分老是被UPDATE那就不要建了,用别的手段来优化积分的查询需求
特别是那些二三十个字段的大表,或多或少有5~10个字段被加了索引,每次(每执行一条增删改SQL语句)有变动就重构索引,重构要时间,下一次的SQL要等待重构完后才能执行,所以就大大阻塞了查询的时间!导致查询变慢
值重复率大的字段不应建索引 ¶
先说优势
索引的优势体现在树的高度赵大,就能为更多数据查询在很少的节点跳转次数中快速找到目标数据的磁盘地址
有成本
建立索引就是要建立一个二叉树数据结构然后保存起来,查询的时候用起来,那它也是占据磁盘空间来存放的,所以不能乱建,要看情况建
值范围的考量
比如有个type字段,值的范围就是1、2、3这样,那在二叉树上也就是3个点,顶部根节点是2,左边是1,右边是3,每个节点里面储存了这些值对应的记录的磁盘地址
可以说这是一棵很矮的二叉树,如果记录有100万条,那这棵矮树就会在3个节点中储存100万条记录的磁盘地址,成为了一棵又矮又胖(占空间)的二叉树,既然100万条记录中type值是1、2、3这样很容易碰到重复值的话,那扫全表去找这些值的损耗成本其实也跟这棵又矮又胖的树的储存、加载成本差不多;再者考虑到记录变化后导致的索引重构成本问题(带来的性价比不高),那还是不要这个type索引好了
选择性
在专业角度有个概念叫选择性,选择性是由
不同值的数量 / 表的记录条数得出的,比如type字段不同值的数量是3,但记录条数有1000,那选择性就是3/1000也就是0.003,这么低的选择性是不值得建立索引的话说选择性要多少才合适呢?这里好像没有固定的说法,应该是看具体的情况吧,我暂时没有找到相关的指导,以及缺少实践,在这方面未来会进一步关注
相关深入阅读 ¶
推荐阅读《MySQL索引背后的数据结构及算法原理》,其实我这里的内容有好些是参照了这篇文章的